А.И.
Орлов
Теория принятия решений
Учебное пособие. - М.: Издательство "Март", 2004.
| Предыдущая |
2. ОПИСАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
2.3.5. Сравнение методов оценивания параметров
В теории оценивания параметров классической математической статистики установлено, что метод максимального правдоподобия, как правило, лучше (в смысле асимптотической дисперсии асимптотического среднего квадрата ошибки), чем метод моментов. Однако в интервальной статистике это, вообще говоря, не так, что продемонстрировано выше на примере оценивания параметров гамма-распределения. Сравним эти два метода оценивания в случае интервальных данных в общей постановке. Поскольку метод максимального правдоподобия – частный случай метода минимального контраста, начнем с разбора этого несколько более общего метода.
Оценки минимального контраста. Пусть Х – пространство,
в котором лежат независимые одинаково распределенные случайные элементы
Будем оценивать
элемент пространства параметров 
с помощью функции
контраста 
Оценкой минимального
контраста называется
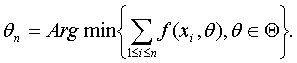
Если множество 
состоит из
более чем одного элемента, то оценкой минимального контраста называют
также любой элемент .
Оценками минимального контраста являются, в частности, многие
робастные статистики [3,36]. Эти оценки широко используются в статистике объектов
нечисловой природы [3,27], поскольку при 
переходят в переходят
в эмпирические средние, а если - пространство
бинарных отношений – в медиану Кемени.
Пусть в Х имеется мера 
(заданная на той
же 
-алгебре,
что участвует в определении случайных элементов xi
), и 
- плотность распределения
xi по мере . Если
то оценка минимального контраста переходит в оценку максимального правдоподобия.
Асимптотическое поведение оценок минимального контраста в
случае пространств Х и общего вида хорошо
изучено [37], в частности, известны условия состоятельности оценок. Здесь ограничимся
случаем X = R1, но при этом введя
погрешности измерений 
Примем также, что
В рассматриваемой математической модели предполагается, что
статистику известны лишь искаженные значения 
Поэтому вместо
он вычисляет
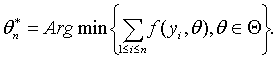
Будем изучать величину 
в предположении,
что погрешности измерений 
малы. Цель этого
изучения – продемонстрировать идеи статистики интервальных данных при достаточно
простых предположениях. Поэтому естественно следовать условиям и ходу рассуждений,
которые обычно принимаются при изучении оценок максимального правдоподобия [38,
п.33.3].
Пусть 
- истинное значение
параметра, функция 
трижды дифференцируема
по 
, причем
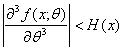
при всех 
Тогда
(27)
где 
Используя обозначения векторов x = (x1 , x2 , ..., xn ), y = (y1 , y2 , ..., yn ), введем суммы
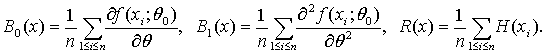
Аналогичным образом введем функции B0(y), B1(y), R(y), в которых вместо xi стоят yi, i=1,2,…,n.
Поскольку в соответствии с теоремой Ферма оценка минимального
контраста удовлетворяет уравнению
(28)
то, подставляя в (27) xi вместо x и суммируя по i = 1,2,…,n, получаем, что
(29)
откуда
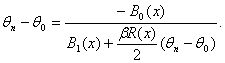(30)
Решения уравнения (28) будем также называть оценками минимального контраста. Хотя уравнение (28) – лишь необходимое условие минимума, такое словоупотребление не будет вызывать трудностей.
Теорема 1. Пусть для любого x выполнено соотношение
(27). Пусть для случайной величины х1
с распределением, соответствующим значению параметра 
существуют математические
ожидания
(31)
Тогда существуют оценки минимального контраста такие, что
при
(в
смысле сходимости по вероятности).
Доказательство. Возьмем 
и 
В силу закона больших
чисел (теорема Хинчина) существует 
такое, что для
любого 
справедливы неравенства
Тогда с вероятностью не менее 
одновременно выполняются
соотношения
(32)
При
рассмотрим многочлен
второй степени
(см. формулу (29)). С вероятностью не менее выполнены соотношения
Если 
то знак 
в точках
и 
определяется знаком
линейного члена 
следовательно,
знаки 
и 
различны, а потому
существует 
такое, что
что
и требовалось доказать.
Теорема 2. Пусть выполнены условия теоремы 2 и, кроме
того, для случайной величины х1,
распределение которой соответствует значению параметра существует математическое
ожидание
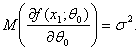
Тогда оценка минимального контраста имеет асимптотически нормальное распределение:
(33)
для любого х, где Ф(x) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Доказательство. Из центральной предельной теоремы вытекает,
что числитель в правой части формулы (30) асимптотически нормален с математическим
ожиданием 0 и дисперсией 
Первое слагаемое
в знаменателе формулы (30) в силу условий (31) и закона больших чисел сходится
по вероятности к 
а второе слагаемое
по тем же основанием и с учетом теоремы 1 – к 0. Итак, знаменатель сходится
по вероятности к 
Доказательство
теоремы 2 завершает ссылка на теорему о наследовании сходимости [3,параграф
2.4].
Нотна оценки минимального контраста. Аналогично (30) нетрудно получить, что
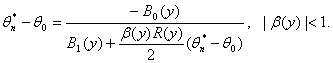(34)
Следовательно, 
есть разность правых
частей формул (30) и (34). Найдем максимально возможное значение (т.е. нотну)
величины 
при ограничениях
(1) на абсолютные погрешности результатов измерений.
Покажем, что при 
для некоторого
C>0 нотна
имеет вид
(35)
Поскольку 
то из (33) и (35)
следует, что
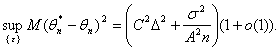(36)
Можно сказать, что наличие погрешностей приводит к появлению
систематической ошибки (смещения) у оценки метода максимального правдоподобия,
и нотна является максимально возможным значением этой
систематической ошибки.
В правой части (36) первое слагаемое – квадрат асимптотической нотны, второе соответствует статистической ошибке. Приравнивая их, получаем рациональный объем выборки
Остается доказать соотношение (35) и вычислить С. Укажем
сначала условия, при которых 
(по вероятности)
при одновременно с
Теорема 3. Пусть существуют константа 
и функции g1(x), g2(x), g3(x) такие, что при
и 
выполнены неравенства
(ср. формулу (27))
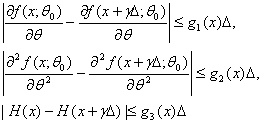…(37)
при всех x. Пусть для случайной величины х1, распределение которой соответствует
, существуют m1 = Mg1(x1), m2 = Mg2(x1) и m3 = Mg3(x1). Пусть выполнены условия
теоремы 1. Тогда (по вероятности)
при , .
Доказательство проведем по схеме доказательства теоремы 1. Из неравенств (37) вытекает, что
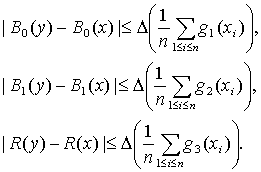(38)
Возьмем и В силу закона больших
чисел (теорема Хинчина) существует такое, что для
любого справедливы неравенства
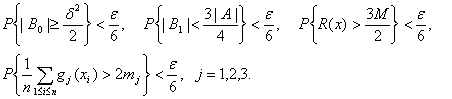
Тогда с вероятностью не менее одновременно выполняются
соотношения
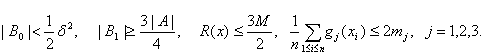
В силу (38) при этом
Пусть
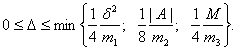
Тогда с вероятностью не менее одновременно выполняются
соотношения (ср. (32))
Завершается доказательство дословным повторением такового в теореме 1, с единственным отличием – заменой в обозначениях x на y.
Теорема 4. Пусть выполнены условия теоремы 3 и, кроме
того, существуют математические ожидания (при
)
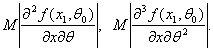(39)
Тогда выполнено соотношение (35) с
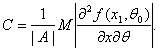(40)
Доказательство. Воспользуемся следующим элементарным соотношением. Пусть a и b – бесконечно малые по сравнению с Z и B соответственно. Тогда с точностью до бесконечно малых более высокого порядка
Чтобы применить это соотношение к анализу в соответствии
с (30), (34) и теоремой 2, положим
В силу условий
теоремы 4 при малых с точностью до
членов более высокого порядка
При эти величины бесконечно
малы, а потому с учетом сходимости B1(x) к А и теоремы 3
с точностью до бесконечно малых более высокого порядка, где
Ясно, что задача оптимизации
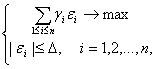(41)
имеет решение
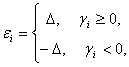
при этом максимальное значение линейной формы есть 
Поэтому
(42)
С целью упрощения правой части (42) воспользуемся тем, что
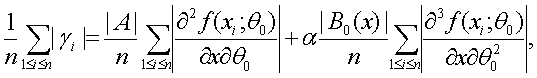(43)
где 
Поскольку при
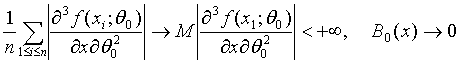
по вероятности, то второе слагаемое в (43) сходится к 0, а первое в силу закона больших чисел с учетом (39) сходится к СА2, где С определено в (40). Теорема 4 доказана.
Оценки метода моментов. Пусть 
- некоторые функции.
Рассмотрим аналоги выборочных моментов
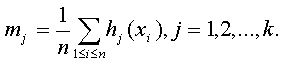
Оценки метода моментов имеют вид
(функции g и hj должны удовлетворять некоторым дополнительным условиям [, с.80], которые здесь не приводим). Очевидно, что
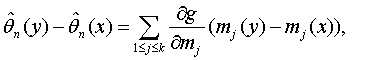
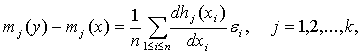(44)
с точностью до бесконечно малых более высокого порядка, а потому с той же точностью
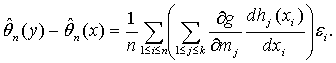(45)
Теорема 5. Пусть при
существуют математические
ожидания
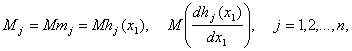
функция g дважды непрерывно
дифференцируема в некоторой окрестности точки 
Пусть существует
функция 
такая, что
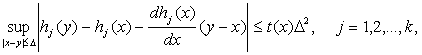(46)
причем Mt(x1) существует. Тогда
с точностью до бесконечно малых более высокого порядка, причем
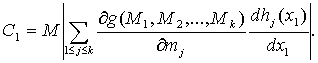
Доказательство теоремы 5 сводится к обоснованию проведенных
ранее рассуждений, позволивших получить формулу (45). В условиях теоремы 5 собраны
предположения, достаточные для такого обоснования. Так, условие (46) дает возможность
обосновать соотношения (44); существование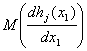 
обеспечивает существование
С1, и т.д. Завершает доказательство ссылка на
решение задачи оптимизации (41) и применение закона больших чисел.
Полученные в теоремах 4 и 5 нотны
оценок минимального контраста и метода моментов, асимптотические дисперсии этих
оценок (см. теорему 2 и [40] соответственно) позволяют находить рациональные
объемы выборок, строить доверительные интервалы с учетом погрешностей измерений,
а также сравнивать оценки по среднему квадрату ошибки (36). Подобное сравнение
было проведено для оценок максимального правдоподобия и метода моментов параметров
гамма-распределения. Установлено, что классический
вывод о преимуществе оценок максимального правдоподобия [33, с.99-100] неверен
в случае 
| Предыдущая |