8.4. Законы больших чисел и состоятельность статистических оценок в пространствах произвольной природы

Законы больших чисел состоят в том, что эмпирические средние сходятся к теоретическим. В классическом варианте: выборочное среднее арифметическое при определенных условиях сходится по вероятности при росте числа слагаемых к математическому ожиданию. На основе законов больших чисел обычно доказывают состоятельность различных статистических оценок. В целом эта тематика занимает заметное место в теории вероятностей и математической статистике.

Однако математический аппарат при этом основан на свойствах сумм случайных величин (векторов, элементов линейных пространств). Следовательно, он не пригоден для изучения вероятностных и статистических проблем, связанных со случайными объектами нечисловой природы. Это такие объекты, как бинарные отношения, нечеткие множества, вообще элементы пространств без векторной структуры. Объекты нечисловой природы все чаще встречаются в прикладных исследованиях. Много конкретных примеров приведено выше в настоящей главе. Поэтому представляется полезным получение законов больших чисел в пространствах нечисловой природы. Необходимо решить следующие задачи.

А) Определить понятие эмпирического среднего.

Б) Определить понятие теоретического среднего.

В) Ввести понятие сходимости эмпирических средних к теоретическому.

Г) Доказать при тех или иных комплексах условий сходимость эмпирических средних к теоретическому.

Д) Обобщив это доказательство, получить метод обоснования состоятельности различных статистических оценок.

Е) Дать применения полученных результатов при решении конкретных задач.

Ввиду принципиальной важности рассматриваемых результатов приводим доказательство закона больших чисел, а также результаты компьютерного анализа множества эмпирических средних.

Определения средних величин. Пусть X - пространство произвольной природы, x₁, x₂, x₃,...,x_n - его элементы. Чтобы ввести эмпирическое среднее для x₁, x₂, x₃,...,x_n будем использовать действительнозначную (т.е. с числовыми значениями) функцию f(x,y) двух переменных со значениями в X. В стандартных математических обозначениях, Величина f(x,y) интерпретируется как показатель различия между x и y: чем f(x,y) больше, тем x и y сильнее различаются. В качестве f можно использовать расстояние в Х, квадрат расстояния и т.п.

Определение 1. Средней величиной для совокупности x₁, x₂, x₃,...,x_n (относительно меры различия f), обозначаемой любым из трех способов:

хср = En(f) = En(x₁, x₂, x₃,...,x_n ; f) ,

называем решение оптимизационной задачи

Это определение согласуется с классическим: если Х = R1, f(x,y) = (x - y)2, то хср - выборочное среднее арифметическое. Если же Х = R1, f(x,y) = |x - y|, то при n = 2k+1 имеем хср = x(k+1), при n= 2k эмпирическое среднее является отрезком [x(k), x(k+1)]. Здесь через x(i) обозначен i-ый член вариационного ряда, построенного по x₁, x₂, x₃,...,x_n, т.е. i-я порядковая статистика. Таким образом, при Х = R1, f(x,y) = |x - y| решение задачи (1) дает естественное определение выборочной медианы, правда, несколько отличающееся от предлагаемого в курсах "Общей теории статистики", в котором при n= 2k медианой называют полусумму двух центральных членов вариационного ряда (x(k) + x(k+1))/2. Иногда x(k) называют левой медианой , а х(k+1) - правой медианой [3].

Решением задачи (1) является множество En(f), которое может быть пустым, состоять из одного или многих элементов. Выше приведен пример, когда решением является отрезок. Если Х = R1 \ {х₀} , f(x,y) = (x - y)2 , а среднее арифметическое выборки равно х₀, то En(f) пусто.

При моделировании реальных ситуаций часто можно принять, что Х состоит из конечного числа элементов, а тогда En(f) непусто - минимум на конечном множестве всегда достигается.

 Понятия случайного элемента  со значениями в Х, его распределения, независимости случайных элементов используем согласно пункту 2 настоящей главы, т.е. справочнику Ю.В. Прохорова и Ю.А. Розанова [25]. Будем считать, что функция f измерима относительно -алгебры, участвующей в определении случайного элемента . Тогда  при фиксированном y является действительнозначной случайной величиной. Предположим, что она имеет математическое ожидание.

Определение 2. Теоретическим средним (математическим ожиданием) для случайного элемента  относительно меры различия f, обозначаемом E(x,f), называется решение оптимизационной задачи

Это определение также согласуется с классическим. Если Х = R1, f(x,y) = (x - y)2, то E(x,f) = E(x) - обычное математическое ожидание, при этом E - дисперсия случайной величины . Если же Х = R1 , f(x,y) = |x - y| , то E(x,f) = [a,b], где a = sup{t: F(t)<0,5}, b = inf{t: F(t)>0,5}, причем F(t) - функция распределения случайной величины . Если график F(t) имеет плоский участок на уровне F(t) = 0,5, то медиана - теоретическое среднее в смысле определения 2 - является отрезком. В классическом случае обычно говорят, что каждый элемент отрезка [a; b] является одним из возможных значений медианы. Поскольку наличие указанного плоского участка - исключительный случай, то обычно решением задачи (2) является множество из одного элемента a = b - классическая медиана распределения случайной величины .

Теоретическое среднее E(x,f) можно определить лишь тогда, когда  существует при всех . Оно может быть пустым множеством, например, если Х = R1 \ {х₀} , f(x,y) = (x - y)2 , x₀= E(x). И то, и другое исключается, если Х конечно. Однако и для конечных Х теоретическое среднее может состоять не из одного, а из многих элементов. Отметим, однако, что в множестве всех распределений вероятностей на Х подмножество тех распределений, для которых E(x,f) состоит более чем из одного элемента, имеет коразмерность 1, поэтому основной является ситуация, когда множество E(x,f) содержит единственный элемент [3].

Существование средних величин. Под существованием средних величин будем понимать непустоту множеств решений соответствующих оптимизационных задач.

Если Х состоит из конечного числа элементов, то минимум в задачах (1) и (2) берется по конечному множеству, а потому, как уже отмечалось, эмпирические и теоретические средние существуют.

Ввиду важности обсуждаемой темы приведем доказательства. Для строгого математического изложения нам понадобятся термины из раздела математики под названием "общая топология". Топологические термины и результаты будем использовать в соответствии с классической монографией [29]. Так, топологическое пространство называется бикомпактным в том и только в том случае, когда из каждого его открытого покрытия можно выбрать конечное подпокрытие [29, с.183]..

Теорема 1. Пусть Х - бикомпактное пространство, функция f непрерывна на Х2 (в топологии произведения). Тогда эмпирическое и теоретическое средние существуют.

Доказательство. Функция f(xi,y) от y непрерывна, сумма непрерывных функций непрерывна, непрерывная функция на бикомпакте достигает своего минимума, откуда и следует заключение теоремы относительно эмпирического среднего.

Перейдем к теоретическому среднему. По теореме Тихонова [29, с.194] из бикомпактности Х вытекает бикомпактность Х2. Для каждой точки (x, y) из Х2 рассмотрим  - окрестность в Х2 в смысле показателя различия f, т.е. множество

Поскольку f непрерывна, то множества U(x,y) открыты в рассматриваемой топологии в Х2. По теореме Уоллеса [29, с.193] существуют открытые (в Х) множества V(x) и W(y), содержащие x и y соответственно и такие, что их декартово произведение V(x) x W(y) целиком содержится внутри U(x, y).

Рассмотрим покрытие Х2 открытыми множествами V(x) x W(y). Из бикомпактности Х2 вытекает существование конечного подпокрытия {V(xi) x W(yi), i = 1,2,...,m}. Для каждого х из Х рассмотрим все декартовы произведения V(xi) x W(yi), куда входит точка (x, y) при каком-либо y. Таких декартовых произведений и их первых множителей V(xi) конечное число. Возьмем пересечение таких первых множителей V(xi) и обозначим его Z(x). Это пересечение открыто, как пересечение конечного числа открытых множеств, и содержит точку х. Из покрытия бикомпактного пространства X открытыми множествами Z(x) выберем открытое подпокрытие Z1, Z2, ..., Zk.

Покажем, что если  и  принадлежат одному и тому же Zj при некотором j, то

         (3)

Пусть Zj = Z(x₀) при некотором x₀. Пусть V(xi) x W(yi), , - совокупность всех тех исходных декартовых произведений из системы {V(xi) x W(yi), i = 1,2,...,m}, куда входят точки (x₀, y) при различных y. Покажем, что их объединение содержит также точки  и  при всех y. Действительно, если (х₀, y) входит в V(xi) x W(yi), то y входит в W(yi), а  и  вместе с x₀ входят в V(xi), поскольку ,  и x₀ входят в Z(x₀). Таким образом,  и  принадлежат V(xi) x W(yi), а потому согласно определению V(xi) x W(yi)

откуда и следует неравенство (3).

Поскольку Х2 - бикомпактное пространство, то функция f ограничена на Х2 , а потому существует математическое ожидание E f(,y) для любого случайного элемента , удовлетворяющего приведенным в предыдущем разделе условиям согласования топологии, связанной с f, и измеримости, связанной с . Если х₁ и х₂ принадлежат одному открытому множеству Zj , то

а потому функция

g(y) = E f(,y)       (4)

непрерывна на Х. Поскольку непрерывная функция на бикомпактном множестве достигает своего минимума, т.е. существуют такие точки z, на которых g(z) = inf{g(y), yX}, то теорема 1 доказана.

В ряде интересных для приложений ситуаций Х не является бикомпактным пространством. Например, если Х = R1. В этих случаях приходится наложить на показатель различия f некоторые ограничения, например, так, как это сделано в теореме 2.

Теорема 2. Пусть Х - топологическое пространство, непрерывная (в топологии произведения) функция f: X2R1 неотрицательна, симметрична (т.е. f(x,y) = f (y,x) для любых x и y из X), существует число D>0 такое, что при всех x,y,z из X

f(x,y) < D{f(x,z) + f(z,y)}.        (5)

Пусть в Х существует точка x₀ такая, что при любом положительном R множество{x: f(x, x₀) <R} является бикомпактным. Пусть для случайного элемента , согласованного с топологией в рассмотренном выше смысле, существует g(x₀) = Ef(, x₀ ).

Тогда существуют (т.е. непусты) математическое ожидание E(x,f) и эмпирические средние En(f).

Замечание. Условие (5) - некоторое обобщение неравенства треугольника. Например, если g - метрика в X, а f = gp при некотором натуральном p, то для f выполнено соотношение (5) с D = 2p.

Доказательство. Рассмотрим функцию g(y), определенную формулой (4). Имеем

f(,y) < D {f(, x₀) + f(x₀,,y)}.         (6)

Поскольку по условию теоремы g(x₀) существует, а потому конечно, то из оценки (6) следует существование и конечность g(y) при всех y из Х. Докажем непрерывность этой функции.

Рассмотрим шар (в смысле меры различия f ) радиуса R с центром в x₀:

K(R) = {x : f(x, x₀) < R}, R > 0.

В соответствии с условием теоремы K(R) как подпространство топологического пространства Х является бикомпактным. Рассмотрим произвольную точку х из Х. Справедливо разложение

где (С) - индикатор множества С. Следовательно,

           (7)

Рассмотрим второе слагаемое в (7). В силу (5)

          (8)

Возьмем математическое ожидание от обеих частей (8):

        (9)

В правой части (9) оба слагаемых стремятся к 0 при безграничном возрастании R: первое - в силу того, что

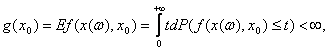
второе - в силу того, что распределение случайного элемента  сосредоточено на Х и

Пусть U(x) - такая окрестность х (т.е. открытое множество, содержащее х), для которой

sup {f(y, x), yU(x)} < 

Имеем

      (10)

В силу (9) и (10) при безграничном возрастании R

      (11)

равномерно по yU(x). Пусть R(0) таково, что левая часть (11) меньше > 0 при R>R(0) и, кроме того, yU(x) K(R(0)). Тогда при R>R(0)

(12)

Нас интересует поведение выражения в правой части формулы (12) при yU(x). Рассмотрим f1 - сужение функции f на замыкание декартова произведения множеств U(x) х K(R), и случайный элемент  Тогда

при yU(x), а непрерывность функции  была доказана в теореме 1. Последнее означает, что существует окрестность U₁(x) точки х такая, что

    (13)

при yU₁(x). Из (12) и (13) вытекает, что при

что и доказывает непрерывность функции g(x).

Докажем существование математического ожидания E(x,f). Пусть R(0) таково, что

      (14)

Пусть H - некоторая константа, значение которой будет выбрано позже. Рассмотрим точку х из множества K(HR(0))^С - дополнения K(HR(0)), т.е. из внешности шара радиуса HR(0) с центром в х₀. Пусть Тогда имеем

откуда

     (15)

Выбирая H достаточно большим, получим с учетом условия (14), что при xK(HR(0))^С справедливо неравенство

      (16)

Можно выбрать H так, чтобы правая часть (16) превосходила

Сказанное означает, что Argmin g(x) достаточно искать внутри бикомпактного множества K(HR(0)). Из непрерывности функции g вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем Х. Существование (непустота) теоретического среднего E(x,f) доказана.

Докажем существование эмпирического среднего En(f). Есть искушение проводить его дословно так же, как и доказательство существования математического ожидания E(x,f), лишь с заменой 1/2 в формуле (16) на частоту попадания элементов выборки xi в шар K(R(0)), каковая, очевидно, стремится к вероятности попадания случайного элемента  в K(R(0)), большей 1/2 в соответствии с (14). Однако это рассуждение показывает лишь, что вероятность непустоты En(f) стремится к 1 при безграничном росте объема выборки. Точнее, оно показывает, что

Поэтому пойдем другим путем, не опирающимся к тому же на вероятностную модель выборки. Положим

    (17)

Если х входит в дополнение шара K(HR(1)), то аналогично (15) имеем

       (18)

При достаточно большом H из (17) и (18) следует, что

Следовательно, Argmin достаточно искать на K(HR(1)). Заключение теоремы 2 следует из того, что на бикомпактном пространстве K(HR(1)) минимизируется непрерывная функция.

Теорема 2 полностью доказана.

О формулировках законов больших чисел. Пусть  - независимые одинаково распределенные случайные элементы со значениями в Х. Закон больших чисел - это утверждение о сходимости эмпирических средних к теоретическому среднему (математическому ожиданию) при росте объема выборки n, т.е. утверждение о том, что

  (19)

при . Однако и слева, и справа в формуле (19) стоят, вообще говоря, множества. Поэтому понятие сходимости в (19) требует обсуждения и определения.

В силу классического закона больших чисел при

       (20)

в смысле сходимости по вероятности, если правая часть существует (теорема А.Я. Хинчина, 1923 г.).

Если пространство Х состоит из конечного числа элементов, то из соотношения (20) легко вытекает (см., например, [3, с.192-193]), что

  (21)

Другими словами,  является состоятельной оценкой .

Если  состоит из одного элемента, , то соотношение (21) переходит в следующее:

       (22)

Однако с прикладной точки зрения доказательство соотношений (21)-(22) не дает достаточно уверенности в возможности использования  в качестве оценки E(x,f), поскольку в процессе доказательства объем выборки предполагается настолько большим, что при всех yX одновременно левые части соотношений (20) сосредотачиваются в непересекающихся окрестностях правых частей.

Замечание. Если в соотношении (20) рассмотреть сходимость с вероятностью 1, то аналогично (21) получим т.н. усиленный закон больших чисел [3, с.193-194], согласно которому с вероятностью 1 эмпирическое среднее  входит в теоретическое среднее E(x,f), начиная с некоторого объема выборки n, вообще говоря, случайного, . Мы не будем останавливаться на этом виде сходимости, поскольку в соответствующих постановках, подробно разобранных в монографии [3], нет принципиальных отличий от случая сходимости по вероятности.

Если Х не является конечным, например, Х = R1 , то соотношения (21) и (22) неверны. Поэтому необходимо искать иные формулировки закона больших чисел. В классическом случае сходимости выборочного среднего арифметического к математическому ожиданию, т.е.  можно записать закон больших чисел так: для любого  > 0 справедливо предельное соотношение

  (23)

В этом соотношении в отличие от (21) речь идет о попадании эмпирического среднего = не непосредственно внутрь теоретического среднего E(x,f), а в некоторую окрестность теоретического среднего.

Обобщим эту формулировку. Как задать окрестность теоретического среднего в пространстве произвольной природы? Естественно взять его окрестность, определенную с помощью какой-либо метрики. Однако полезно обеспечить на ее дополнении до Х отделенность множества значений Ef(x(),y) как функции y от минимума этой функции на всем Х.

Поэтому мы сочли целесообразным определить такую окрестность с помощью самой функции Ef(x(),y).

Определение 3. Для любого > 0 назовем -пяткой функции g(x) множество

Таким образом, в -пятку входят все те х, для которых значение g(x) либо минимально, либо отличается от минимального (или от инфимума) не более чем на . Так, для X = R1 и функции g(x) = х2 минимум равен 0, а -пятка имеет вид интервала . В формулировке (23) классического закона больших чисел утверждается, что при любом >0 вероятность попадания среднего арифметического в -пятку математического ожидания стремится к 1. Поскольку > 0 произвольно, то вместо -пятки можно говорить о -пятке, т.е. перейти от (23) к эквивалентной записи

      (24)

Соотношение (24) допускает непосредственное обобщение на общий случай пространств произвольной природы.

СХЕМА ЗАКОНА БОЛЬШИХ ЧИСЕЛ. Пусть  - независимые одинаково распределенные случайные элементы со значениями в пространстве произвольной природы Х с показателем различия f: X2R1. Пусть выполнены некоторые математические условия регулярности. Тогда для любого > 0 справедливо предельное соотношение

     (25)

Аналогичным образом может быть сформулирована и общая идея усиленного закона больших чисел. Ниже приведены две конкретные формулировки "условий регулярности".

Законы больших чисел. Начнем с рассмотрения естественного обобщения конечного множества - бикомпактного пространства Х.

Теорема 3. В условиях теоремы 1 справедливо соотношение (25).

Доказательство. Воспользуемся построенным при доказательстве теоремы 1 конечным открытым покрытием {Z1, Z2, ..., Zk} пространства Х таким, что для него выполнено соотношение (3). Построим на его основе разбиение Х на непересекающиеся множества W1, W2, ..., Wm (объединение элементов разбиения W1, W2, ..., Wm составляет Х). Это можно сделать итеративно. На первом шаге из Z1 следует вычесть Z2, ..., Zk - это и будет W1 . Затем в качестве нового пространства надо рассмотреть разность Х и W1 , а покрытием его будет {Z2, ..., Zk} . И так до k-го шага, когда последнее из рассмотренных покрытий будет состоять из единственного открытого множества Zk . Остается из построенной последовательности W1, W2, ..., Wk вычеркнуть пустые множества, которые могли быть получены при осуществлении описанной процедуры (поэтому, вообще говоря, m может быть меньше k).

В каждом из элементов разбиения W1, W2, ..., Wm выберем по одной точке, которые назовем центрами разбиения и соответственно обозначим w1, w2, ..., wm. Это и есть то конечное множество, которым можно аппроксимировать бикомпактное пространство Х. Пусть y входит в Wj . Тогда из соотношения (3) вытекает, что

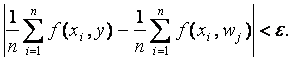          (26)

Перейдем к доказательству соотношения (25). Возьмем произвольное >0. Рассмотрим некоторую точку b из E(x,f). Доказательство будет основано на том, что с вероятностью, стремящейся к 1, для любого y вне  выполнено неравенство

(27)

Для обоснования этого неравенства рассмотрим все элементы разбиения W1, W2, ..., Wm, имеющие непустое пересечение с внешностью -пятки . Из неравенства (26) следует, что для любого y вне  левая часть неравенства (27) не меньше

      (28)

где минимум берется по центрам всех элементов разбиения, имеющим непустое пересечение с внешностью -пятки. Возьмем теперь в каждом таком разбиении точку vi , лежащую вне -пятки . Тогда из неравенств (3) и (28) следует, что левая часть неравенства (27) не меньше

     (29)

В силу закона больших чисел для действительнозначных случайных величин каждая из участвующих в соотношениях (27) и (29) средних арифметических имеет своими пределами соответствующие математические ожидания, причем в соотношении (29) эти пределы не менее

поскольку точки vi лежат вне -пятки . Следовательно, при

и достаточно большом n, обеспечивающем необходимую близость рассматриваемого конечного числа средних арифметических к их математическим ожиданиям, справедливо неравенство (27).

Из неравенства (27) следует, что пересечение En(f) с внешностью  пусто. При этом точка b может входить в En(f), а может и не входить. Во втором случае En(f) состоит из иных точек, входящих в . Теорема 3 доказана.

Если Х не является бикомпактным пространством, то необходимо суметь оценить рассматриваемые суммы "на периферии", вне бикомпактного ядра, которое обычно выделяется естественным путем. Один из возможных комплексов условий сформулирован выше в теореме 2.

Теорема 4. В условиях теоремы 2 справедлив закон больших чисел, т.е. соотношение (25).

Доказательство. Будем использовать обозначения, введенные в теореме 2 и при ее доказательстве. Пусть r и R, r < R, - положительные числа. Рассмотрим точку х в шаре K(r) и точку y вне шара K(R). Поскольку

то

      (30)

Положим

Сравним  и . Выборку  разобьем на две части. В первую часть включим те элементы выборки, которые входят в K(r), во вторую - все остальные (т.е. лежащие вне K(r) ). Множество индексов элементов первой части обозначим I = I(n,r). Тогда в силу неотрицательности f имеем

а в силу неравенства (30)

где Card I(n,r) - число элементов в множестве индексов I(n,r). Следовательно,

  (31)

где J = Card I(n,r) - биномиальная случайная величина B(n,p) с вероятностью успеха p = P{}. По теореме Хинчина для  справедлив (классический) закон больших чисел. Пусть . Выберем  так, чтобы при  было выполнено соотношение

    (32)

где  Выберем r так, чтобы вероятность успеха p>0,6. По теореме Бернулли можно выбрать  так, чтобы при

    (33)

Выберем R так, чтобы

Тогда

           (34)

и согласно (31), (32) и (33) при  с вероятностью не менее  имеем

          (35)

для любого y вне K(R). Из (34) следует, что минимизировать  достаточно внутри бикомпактного шара K(R), при этом En(f) не пусто и

           (36)

с вероятностью не менее 1-2.

Пусть  и  - сужения  и g(x) = Ef(x(), x) соответственно на K(R) как функций от х. В силу (34) справедливо равенство  Согласно доказанной выше теореме 3 найдется  такое, что

Согласно (36) с вероятностью не менее

при  Следовательно, при  имеем

что и завершает доказательство теоремы 4.

Справедливы и иные варианты законов больших чисел, полученные, в частности, в статье [27].

Асимптотическое поведение решений экстремальных статистических задач. Если проанализировать приведенные выше постановки и результаты, особенно теоремы 1 и 3, то становится очевидной возможность их обобщения. Так, доказательства этих теорем практически не меняются, если считать, что функция f(x,y) определена на декартовом произведении бикомпактных пространств X и Y. Тогда можно считать, что элементы выборки лежат в Х, а Y - пространство параметров, подлежащих оценке. Пусть, например, выборка взята из распределения с плотностью p(x,y). Если положить

f(x,y) = - ln p(x,y) ,

то задача нахождения эмпирического среднего переходит в задачу оценивания неизвестного параметра y методом максимального правдоподобия, а законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств X и Y общего вида. В случае функции f(x,y) общего вида можно говорить об определении и состоятельности так называемых оценок минимального контраста. Частными случаями этих оценок являются, например, устойчивые (робастные) оценки Тьюки-Хубера (см. главу 10 ниже), оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы.

Можно пойти и дальше в обобщении законов больших чисел. Пусть известно, что при каждом конкретном y при безграничном росте n имеет быть сходимость по вероятности

fn(x(), y )f(y).

В каких случаях и в каком смысле

Argmin {fn(x(), y ), yX}Argmin { f(y), y X} ?

Причем здесь можно под n понимать натуральное число. А можно рассматривать "сходимость по фильтру" в смысле Картана и Бурбаки [29, с.118]. В частности, описывать ситуацию вектором, координаты которого - объемы нескольких выборок, и все они безгранично растут. В классической математической статистике такие постановки рассматривать не любят.

Поскольку, как уже отмечалось, основные задачи прикладной статистики можно представить в виде оптимизационных задач, то ответ на поставленный вопрос дает возможность единообразного подхода к изучению асимптотики решений разнообразных экстремальных статистических задач. Одна из возможных формулировок дана и обоснована выше. Другая - в работе [28]. Она основана на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики. К сожалению, в рамках настоящей главы нет возможности подробнее остановиться на проблеме оценивания.

Рассматриваемую тематику можно развивать дальше, в частности, рассматривать пространства X и Y, не являющиеся бикомпактными, а также изучать скорость сходимости эмпирических средних к теоретическим.

Медиана Кемени и экспертные оценки. Рассмотрим частный случай пространств нечисловой природы - пространство бинарных отношений на конечном множестве и его подпространства. Как известно, каждое бинарное отношение А можно описать матрицей ||a(i,j)|| из 0 и 1, причем a(i,j) = 1 тогда и только тогда qi и qj находятся в отношении А, и a(i,j) = 0 в противном случае.

Определение 4. Расстоянием Кемени между бинарными отношениями А и В, описываемыми матрицами ||a(i,j)|| и ||b(i,j)|| соответственно, называется

Замечание. Иногда в определение расстояния Кемени вводят множитель, зависящий от k.

Как уже отмечалось, указанное расстояние введено американским исследователем Дж. Кемени в 1950-х годах и получило в нашей стране известность благодаря монографии [24], в которой оно получено для упорядочений (т.е. ранжировок, в которых допускаются связи, или кластеризованных ранжировок - см. главу 12) исходя из некоторой системы аксиом. Некоторое время казалось, что аксиоматический подход избавляет от субъективизма в выборе расстояния, а потому - от субъективизма в выборе способа усреднения бинарных отношений. Монография [24] породила поток работ, в которых с помощью различных систем аксиом вводились те или иные расстояния в пространствах объектов нечисловой природы (в обзоре [23] на эту тему - 161 ссылка на соответствующие публикации). В итоге произвол в выборе метрик отодвинут на уровень произвола в выборе систем аксиом.

Определение 5. Медианой Кемени для выборки, состоящей из бинарных отношений, называется эмпирическое среднее, построенное с помощью расстояния Кемени.

Поскольку число бинарных отношений на конечном множестве конечно, то эмпирические и теоретические средние для произвольных показателей различия существуют и справедливы законы больших чисел, описанные формулами (21) и (22) выше.

Бинарные отношения, в частности, упорядочения, часто используются для описания мнений экспертов. Тогда расстояние Кемени измеряет близость мнений экспертов, а медиана Кемени позволяет находить итоговое усредненное мнение комиссии экспертов. Расчет медианы Кемени обычно включают в информационное обеспечение систем принятия решений с использованием оценок экспертов. Речь идет, например, о математическом обеспечении автоматизированного рабочего места "Математика в экспертизе" (АРМ "МАТЭК"), предназначенного, в частности, для использования при проведении экспертиз в задачах экологического страхования. Поэтому представляет большой практический интерес численное изучение свойств медианы Кемени при конечном объеме выборки. Такое изучение дополняет описанную выше асимптотическую теорию, в которой объем выборки предполагается безгранично возрастающим ().

Компьютерное изучение свойств медианы Кемени при конечных объемах выборок. С помощью специально разработанной программной системы В.Н. Жихаревым был проведен ряд серий численных экспериментов по изучению свойств выборочных медиан Кемени. Представление о полученных результатах дается приводимой ниже табл.1, взятой из статьи [30]. В каждой серии методом статистических испытаний определенное число раз моделировался случайный и независимый выбор экспертных ранжировок, а затем находились все медианы Кемени для смоделированного набора мнений экспертов. При этом в сериях 1-5 распределение ответа эксперта предполагалось равномерным на множестве всех ранжировок, а в серии 6 это распределение являлось монотонным относительно расстояния Кемени с некоторым центром (о понятии монотонности см. выше), т.е. вероятность выбора определенной ранжировки убывала с увеличением расстояния Кемени этой ранжировки от центра. Таким образом, серии 1-5 соответствуют ситуации, когда у экспертов нет почвы для согласия, нет группировки их мнений относительно некоторого единого среднего группового мнения, в то время как в серии 6 есть единое мнение - описанный выше центр, к которому тяготеют ответы экспертов.

Результаты, приведенные в табл.1, можно комментировать разными способами. Неожиданным явилось большое число элементов в выборочной медиане Кемени - как среднее, так и особенно максимальное. Одновременно обращает на себя внимание убывание этих чисел при росте числа экспертов и особенно при переходе к ситуации реального существования группового мнения (серия 6). Достаточно часто один из ответов экспертов входит в медиану Кемени (т.е. пересечение множества ответов экспертов и медианы Кемени непусто), а диаметр медианы как множества в пространстве ранжировок заметно меньше диаметра множества ответов экспертов. По этим показателям - наилучшее положение в серии 6. Грубо говоря, всяческие "патологии" в поведении медианы Кемени наиболее резко проявляются в ситуации, когда ее применение не имеет содержательного обоснования, т.е. когда у экспертов нет основы для согласия, их ответы равномерно распределены на множестве ранжировок.

Увеличение числа испытаний в 10 раз при переходе от серии 1 к серии 5 не очень сильно повлияло на приведенные в таблице характеристики, поэтому представляется, что суть дела выявляется при числе испытаний (в методе Монте-Карло), равном 100 или даже 50. Увеличение числа объектов или экспертов увеличивает число элементов в рассматриваемом пространстве ранжировок, а потому уменьшается частота попадания какого-либо из мнений экспертов внутрь медианы Кемени, а также отношение диаметра медианы к диаметру множества экспертов, число элементов медианы Кемени (среднее и максимальное). Можно сказать, что увеличение числа объектов или экспертов уменьшает степень дискретности задачи, приближает ее к непрерывному случаю, а потому уменьшает выраженность различных "патологий".

Есть много интересных результатов, которые мы здесь не рассматриваем. Они связанны, в частности, со сравнением медианы Кемени с другими методами усреднения мнений экспертов, например, с нахождением итогового упорядочения по методу средних рангов, а также с использованием малых окрестностей ответов экспертов для поиска входящих в медиану ранжировок, с теоретической и численной оценкой скорости сходимости в законах больших чисел.

Табл.1. Вычислительный эксперимент по изучению свойств медианы Кемени

Номер серии	1	2	3	4	5	6
Число испытаний	100	1000	50	50	1000	1000
Количество объектов	5	5	7	7	5	5
Количество экспертов	10	30	10	30	10	10
Частота непустого пересечения	0,85	0,58	0,52	0,2	0,786	0,911
Среднее отношение диаметров	0.283	0,124	0,191	0,0892	0,202	0.0437
Средняя мощность медианы	5,04	2,41	6,4	2,88	3,51	1,35
Максимальная. мощность медианы	30	14	19	11	40	12