Современное состояние зерноперерабатывающих предприятий Республики Татарстан

Мансуров Руслан Евгеньевич,

кандидат экономических наук,

заместитель директора научно-исследовательского института,

доцент кафедры маркетинга и экономики ИЭУП

(Russell_1@mail.ru)

Аннотация: В статье проведен анализ современного состояния зерноперерабатывающих предприятий Республики Татарстан. В качестве результативного показателя эффективности деятельности зерноперерабатывающих предприятий была выбрана окупаемость затрат на 1 рубль валового производства. Выявлено, что основными  резервами роста результативного показателя являются: фонд оплаты труда работников, занятых в производстве, рост количества инноваций, текучесть кадров.

Ключевые слова: агропромышленный комплекс, зерноперерабатывающие предприятия, экономическая эффективность, инновации, анализ современного состояний АПК

В современных условиях, проблемы эффективного функционирования агропромышленного комплекса становятся все более актуальными. Мировой финансово-экономический кризис коренным образом отразился на всех сферах его функционирования, вызвав в них развитие и усугубление ряда негативных процессов. Среди наиболее весомых из них падение объемов производства продукции сельского хозяйства и перерабатывающей промышленности, нарушение внутрихозяйственных и отраслевых связей, высокий моральный и физический износ машин и оборудования, деградация трудовых ресурсов. Усугубляет крайне тяжелое финансовое положение ряда предприятий неоптимальная структура расчетов, распространение всевозможных бартерных схем, неплатежи, постоянный рост задолженности перед бюджетом, ограничение и не эффективное использование кредитных ресурсов. Вместе с тем уровень жизни населения региона во многом зависит от состояния и темпов развития агропромышленного комплекса и особенно пищевой, перерабатывающей промышленности. Поэтому актуальным является изучение современного состояния, а также выработка рекомендаций выхода из кризиса.

В данной работе представлены результаты исследования состояния зерноперерабатывающих предприятий Республики Татарстан. В целом по отрасли анализ показал, что в настоящее время сложилась отрицательная тенденция сохранения низкой эффективности производства при сравнительно высоких объемах инвестиций и государственных дотаций. Так, по предприятиям растениеводства Республики Татарстан в сравнении с предприятиями других регионов Приволжского Федерального округа рентабельность продукции ниже на 57,6%. При этом объем инвестиций и государственной финансовой поддержки в отрасль по Республике Татарстан больше на 66,7%, а износ основных фондов меньше на 44,5%.

С целью дальнейшего изучения этой негативной тенденции, используя метод многомерного корреляционно-регрессионного анализа, были определены взаимосвязи между основными показателями деятельности и результирующим показателем, характеризующим эффективность зерноперерабатывающих предприятий. Объектами исследования выступали 5 зерноперерабатывающих предприятий Республики Татарстан за период с 1999 по 2009гг.

Применение этого метода позволит решить две основные задачи:

1.  Создаст возможность определения характера связей между показателями. При этом появится возможность установления математической формулы, выражающей данную связь.

2.  Даст возможность измерить тесноту связи между факторными и результативным признаком с целью установления степени влияния каждого из показателей на конечный результат. Данная задача решается путем определения параметров корреляционно-регрессионного уравнения [1].

В целом каждую систему или процесс можно выразить в форме модели, которую характеризуют два вида показателей (признаков): результативных и факторных. Применение данной методики изложено в [2,3].

В качестве результативного признака корреляционно-регрессионной модели (Y) был принят показатель окупаемости затрат на 1 рубль валового производства, который определяется, как отношение затрат к валовому производству.

В качестве факторных признаков использованы следующие показатели:

х1 – выполнение плана продаж, %;

х2 – численность работников занятых в производстве в расчете на 100 т продукции;

х3 – коэффициент соотношения дебиторской и кредиторской задолженности;

x4 – сумма затрат в расчете на 1 т продукции;

x5 – стоимость основных производственных фондов в расчете на 1 т продукции;

х6 – выход готового продукта, %;

х7 – потери сельскохозяйственного сырья при хранении, транспортировки, %;

х8 – удельные затраты на переработку бракованной продукции, руб/ед;

х9 – вложения в развитие персонала, руб/чел;

х10 – убытки от аварий и отказов по вине персонала, руб/чел;

х11 – текучесть кадров, %;

х12 – соотношение цен с конкурентами, %;

х13 – изменение занимаемой доли рынка, %;

х14 – рост количества новых успешных продуктовых брендов, %;

х15 – фонд оплаты труда работников, занятых в производстве на 1 т продукции;

х16 – рост количества инноваций, %, который в свою очередь определяется как:

где К – рост количества инноваций, %, N_н, N_к – количество инноваций в компании соответственно на начало и конец анализируемого периода.

Для вычисления показателей задачи многомерного корреляционно-регрессионного анализа (МКРА) были использованы следующие основные формулы:

1.  Средние арифметические.

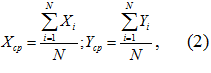
где X_ср, Y_ср – среднеарифметические факторного и результативного признаков;

X, Y – значения признаков одного наблюдения;

i –1,2,3, …, N – индекс значения признака;

N – количество значений признака (количество наблюдений).

2. Среднеквадратичное отклонение.

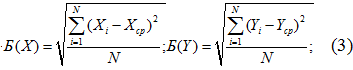
3. Дисперсия.

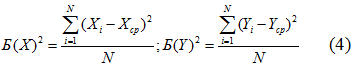
4. Коэффициент вариации по среднеквадратическому отклонению.

5. Коэффициент парной корреляции.

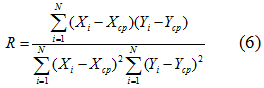
6. Коэффициенты регрессии.

Коэффициенты уравнения множественной линейной регрессии определялись по формулам и методикам, приведенным в [4].

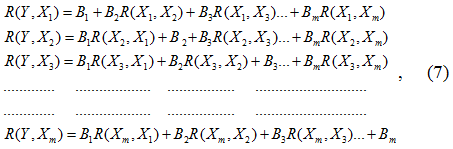
где R(Y,X_i) – парные коэффициенты корреляции между результативным и факторными признаками;

R(X_i,X_j) – парные коэффициенты корреляции между факторными признаками;

В_i – бета-коэффициенты при i, j = 1,2,3, …, m;

m – количество факторных признаков.

Данная система уравнений решалась методом Гаусса относительно бета-коэффициентов - В_i, что позволило рассчитать коэффициенты уравнения множественной линейной регрессии по формулам:

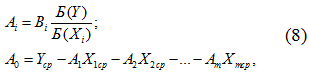
где А_i – (A₀, A₁, A₂,…, A_m) – коэффициенты уравнения множественной регрессии;

Б (Y) – среднеквадратическое отклонение результативного признака;

Б (X_i) – среднеквадратические отклонения факторных признаков (X₁, X₂, X₃,…, X_m);

X_1ср, X_2ср, X_3ср, …, X_mср – среднеарифметические значения факторных признаков;

У_ср – среднеарифметическое значение результативного признака.

7. Бета-коэффициенты.

Данная формула приведена справочно, так как бета-коэффициенты, по предлагаемой методике, определяются как промежуточные величины вычисления коэффициентов регрессии.

8. Ошибка коэффициента корреляции.

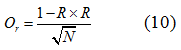
9. Достоверность коэффициента корреляции (критерий Стьюдента)

10. Коэффициент множественной корреляции.

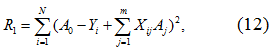
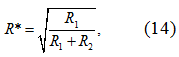
где R* - коэффициент множественной корреляции;

R₁, R₂ – промежуточные значения вычисления – R*.

11. Коэффициент множественной детерминации, %

12. Коэффициент парной детерминации, %

13. Коэффициент отдельного определения, %

Если расчеты выполнены, верно, то коэффициент множественной детерминации должен быть равен сумме коэффициентов отдельного определения, а в парной корреляционной модели коэффициент парной корреляции должен быть равен бета-коэффициенту. Незначительные отклонения в равенствах возможны из-за погрешности вычислений, так как показатели левой и правой частей равенства рассчитывались по различным алгоритмам.

Сначала были определены коэффициенты парной корреляции, ошибка и достоверность коэффициента корреляции. Результаты расчетов представлены в табл. 1.

Значимость, существенность факторов или их адекватность оценивается по t-критерию Стьюдента. Табличное значение t-критерия при 5-ти процентном уровне значимости составляет 2,11. Иными словами при достоверности коэффициента корреляции <2,11 соответствующий коэффициент парной корреляции считается недостоверным. Поэтому такие показатели исключаются из корреляционной модели.

Таблица 1

Значения некоторых параметров корреляционно-регрессионной модели

По данным табл. 1 видно, что показатели х1, х2, х3, x5, х8, х12, х13, х14 необходимо исключить из корреляционной модели, т.к. достоверность коэффициентов корреляции данных показателей <2,11 и они считаются недостоверными.

Таким образом, в процессе дальнейшего исследования необходимо учитывать следующие показатели:

x1 – сумма затрат в расчете на 1 т продукции (бывший x4);

х2 – выход готового продукта, % (бывший x6);

х3 – потери сельскохозяйственного сырья при хранении, транспортировке, % (бывший x7);

х4 – вложения в развитие персонала, руб/чел (бывший x9);

х5 - убытки от аварий и отказов по вине персонала, руб/чел (бывший x10);

х6 – текучесть кадров, % (бывший x11);

х7 – фонд оплаты труда работников, занятых в производстве на 1 т продукции (бывший x15);

х8 – рост количества инноваций, % (бывший x16).

Перечисленные факторы являются существенными, поскольку имеют с результативным фактором значимую связь и коэффициенты парной корреляции достоверны.

Изучение парных межфакторных коэффициентов корреляции осуществлялось с целью установления коллинеарности и мультиколлинеарности (сильной межфакторной связи). При построении и решении производственных функций к факторам предъявляется ряд требований. Одно из основных – это независимость факторов между собой. Согласно классической теории многофакторного корреляционно-регрессионого моделирования связь между факторами уравнения должна отсутствовать. Так Френкель А.А. [5] считает, что два фактора коллинеарные, если парный коэффициент корреляции между ними по абсолютной величине равен или выше 0,8. В рассматриваемой нами модели таких показателей нет.

Результаты произведенных расчетов приведены в табл. 2.

Таблица 2

Основные результаты решения задачи множественной корреляции

Теснота связи между выбранными факторами и полученными в объектах исследования результативными показателями выражена значением коэффициента множественной корреляции (R=0,99). Это свидетельствует о наличии сильной корреляционной связи между окупаемостью затрат на 1 рубль валового производства зерновых перерабатывающих предприятий и влияющими факторами. Множественный коэффициент детерминации равен 98,04 отсюда следует, что на 98,04% изменчивость результативного признака вызвана колебанием названных выше факторов.

Анализ тесноты связи выбранных факторов с результативным показателем позволяет сделать вывод о том, что наиболее сильное влияние на окупаемость затрат зерноперерабатывающих предприятий оказывают показатели: х7 - фонд оплаты труда работников, занятых в производстве на 1 т продукции; х8 - рост количества инноваций, %; х3 - потери сельскохозяйственного сырья при хранении, транспортировке, %.

Среднее влияние на вышеназванный результативный показатель оказывают факторы: х6 - текучесть кадров, %; х4 - вложения в развитие персонала, руб/чел; x1 - сумма затрат в расчете на 1 т продукции; х2 - выход готового продукта, %.

Наиболее слабое влияние оказывает показатель: х5 - убытки от аварий и отказов по вине персонала, руб/чел.

Стоит отметить, что в случае если коэффициент корреляции и бета-коэффициент положительные величины (или оба отрицательные), фактор считается корректным и оставляется в модели. В случае же когда знаки не совпадают, фактор считается некорректным, создающим дополнительную вариацию результативному признак и исключается из модели. В рассматриваемом нами случае значения коэффициентов корреляции и бета-коэффициентов по знаку совпадают.

Важнейшим этапом построения и решения регрессионной модели является установление математической функции. Сложность заключается в том, что из множества функций необходимо найти наиболее достоверно выражающую реально существующие связи между анализируемыми признаками. Опираясь на теоретические знания об изучаемых явлениях, учитывая опыт аналогичных исследований других авторов [2,3] было выбрано следующее уравнение многофакторной линейной корреляционной связи:

где Y – значение результативного признака;

Х₁, Х₂, Х₃, …, Х_n – значения факторных признаков;

а₁, а₂, а₃, …, а_n – коэффициенты регрессии.

Таким образом, уравнение регрессии, полученное в результате решения задачи для зерноперерабатывающих предприятий Республики Татарстан, приобрело вид:

Значения коэффициентов регрессии определяют характер влияния включенных в корреляционную модель факторов на уровень окупаемости затрат на 1 рубль валового производства. В результате решения можно сделать следующие выводы:

1. Теснота связи между факторным (x1 - сумма затрат в расчете на 1 т продукции) и результативным признаками (Y – окупаемость затрат) средняя и прямая (r=0,319). Таким образом, изменчивость результативного признака (Y) на 10,16% зависит от вариации указанного факторного признака. Об этом свидетельствует значение коэффициента детерминации (табл. 2). Коэффициент регрессии указывает на то, что если сумму затрат в расчете на 1 т продукции повысить на 1 %, то это приведет к повышению окупаемости затрат всего на 0,00017%.

2. Парный коэффициент корреляции между выходом готового продукта (x2) и результативным показателем (Y) равен 0,318. Это говорит о наличие слабой, прямой связи между ними. При этом значение Y на 9,79% зависит от влияния данного фактора. Тогда, если выход готового продукта увеличить на 1%, то это приведет к увеличению окупаемости затрат на 0,034%.

3. Теснота связи между показателем потерь сельскохозяйственного сырья при хранении и транспортировке (x3) и Y (окупаемостью затрат) r=-0,361. Это говорит о сильной и обратной связи. В этом случае если потери сельскохозяйственного сырья снизить на 1%, то это приведет к росту окупаемости затрат на 0,078%. При этом изменчивость результативного признака на 13% зависит от колебаний факторного.

4. Теснота связи между вложениями в развитие персонала (х4) и Y сильная и прямая. Влияние данного фактора на 11,4% обуславливает изменение результативного признака (Y). Если затраты на развитие персонала увеличить на 1% в расчете на одного сотрудника, то это приведет к увеличению окупаемости затрат на 0,00007%.

5. Убытки от аварий и отказов по вине персонала (x5) с окупаемостью затрат находятся в обратной, слабой зависимости (r=-0,301), то есть при уменьшении данного показателя в расчете на одного сотрудника на 1% окупаемость затрат практически не вырастет (0,000004%). При этом изменчивость результативного признака на 9,1% зависит от колебаний факторного.

6. Фактор х6 - текучесть кадров оказывает влияние на изменение результативного признака на 12,8%. Теснота связи между показателями средняя и обратная (r=-0,357). Если текучесть кадров будет снижена на 1%, то это приведет к росту окупаемости затрат на 0,011%.

7. Теснота связи х7 - фонд оплаты труда работников, занятых в производстве на 1 т продукции сильная и прямая (r= 0,412). Влияние данного фактора на Y составляет 17%. Если фонд оплаты труда работников, занятых в производстве на 1 т продукции повысить на 1%, то это приведет к росту окупаемости затрат на 0,42%.

8. Рост количества инноваций (x8) с окупаемость затрат находятся в прямой, сильной зависимости. При увеличении данного показателя на 1% окупаемость затрат вырастет на 0,007%. При этом изменчивость результативного признака на 14,17% зависит от колебаний факторного.

Cудя по значению бета-коэффициентов показателей: х7 - фонд оплаты труда работников, занятых в производстве на 1 т продукции (0,414); х8 - рост количества инноваций, % (0,367) и х6 - текучесть кадров, % (-0,359) в них заложены наибольшие резервы роста окупаемости затрат на 1 рубль валового производства зерноперерабатывающих предприятий Республики Татарстан.

Таким образом, в результате проведенного анализа было выявлено, что наиболее сильное влияние на окупаемость затрат зерноперерабатывающих предприятий Республики Татарстан и наибольшие резервы роста данного показателя заложены в фонде оплаты труда работников, росте количества инноваций и потерях сельскохозяйственного сырья при хранении, транспортировке. При этом если влияние оплаты труда и потерь сельскохозяйственного сырья давно установлено, то влияние показателя роста количества инноваций на окупаемость затрат зерноперерабатывающих предприятий Республики Татарстан до настоящего времени не рассматривалось. Хотя в целом только инновационный путь развития способен вывести отечественные агропромышленные предприятия из кризисного состояния. В тоже время инновационность предприятий может развиваться только за счет усиления интеллектуального капитала компании. Подтверждением этому также служат результаты проведенного исследования. Так, наибольшие резервы роста окупаемости затрат на 1 рубль валового производства зерноперерабатывающих предприятий Республики Татарстан кроме роста количества инноваций зависят еще и от фонда оплаты труда и текучести кадров.

Список литературы.

1.  Рабинович, Л.М. Рынок земли: проблемы, поиск, решения / Л.М.Рабинович, В.Г.Тимирясов, А.А.Садретдинова. - Казань: Изд-во «Таглимат» ИЭУП, 2005.

2.   Мухаметгалиев, Ф.Н. Методические подходы к разработке прогнозных моделей развития сельского хозяйства и обеспечения региона продуктами питания на основе изменения демографической ситуации (по материалам Республики Татарстан) / Ф.Н. Мухаметгалиев, Ф.Т. Нежметдинова, Л.Ф. Мухаметгалиева. – М.: РАСХН, 2009.

3.  Хайруллин, А.Н. Факторы корпоративной устойчивости / А.Н.Хайруллин, В.Г.Тимирясов, Л.М.Рабинович. – Казань: Изд-во «Таглимат» ИЭУП, 2006.

4.  Венецкий, И.Г. Основы теории вероятностей и математической статистики / И.Г.Венецкий, Г.С.Кильдишев. – М.: Статистика, 1968. – с.360.

5.  Френкель, А.А. Производительность труда: проблемы моделирования роста / А.А.Френкель. – М.: Экономика, 1984.